数据结构：树篇

发表于 更新于 分类于
本文字数： 3.2k 阅读时长 ≈ 3 分钟

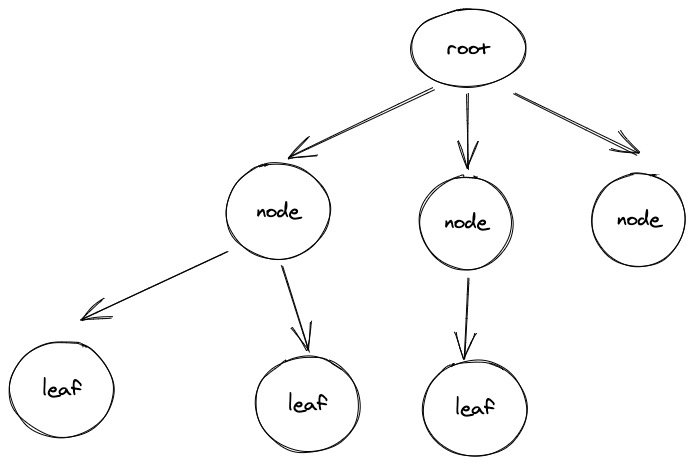
树是一种非线性数据结构。树结构的基本单位是节点。节点之间的链接，称为分支（branch）。节点与分支形成树状，结构的开端，称为根（root），或根结点。根节点之外的节点，称为子节点（child）。没有链接到其他子节点的节点，称为叶节点（leaf）。如下图是一个典型的树结构：

20230418162535

每个节点可以用以下数据结构来表示：

1
2
3
4
Node {
    value: any; // 当前节点的值
    children: Array<Node>; // 指向其儿子
}

一、基本概念

  • 树的高度：节点到叶子节点的最大值就是其高度（叶子节点的高度是 0）
  • 树的深度：高度和深度是相反的，高度是从下往上数，深度是从上往下（根节点的深度是 0）
  • 树的层：根开始定义，根为第一层，根的孩子为第二层
  • N 叉树：每个节点最多只有 N 个子节点的树

二、树的遍历方式

整个树的专题只有一个中心点，那就是树的遍历。通过遍历，我们才得以方便地对树进行搜索和查找等。树的遍历又可以分为两个基本类型，分别是深度优先遍历和广度优先遍历。

深度优先遍历

深度优先搜索方法（Depth-First-Search，以下简称 DFS）是一种用于遍历树或图的算法。沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点 v 的所在边都己被探寻过，搜索将回溯到发现节点 v 的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止，属于盲目搜索。

深度优先遍历图解

算法流程
  1. 首先将根节点放入 stack 中；
  2. 从 stack 中取出第一个节点，并检验它是否为目标。如果找到目标，则结束搜寻并回传结果。否则将它某一个尚未检验过的直接子节点加入 stack 中；
  3. 重复步骤 2；
  4. 如果不存在未检测过的直接子节点。将上一级节点加入 stack 中。重复步骤 2；
  5. 重复步骤 4；
  6. 若 stack 为空，表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。

这里的 stack 可以理解为自己实现的栈，也可以理解为调用栈。如果是调用栈的时候就是递归，如果是自己实现的栈的话就是迭代。

算法模板
1
2
3
4
5
6
7
8
function dfs(root) {
    if (满足特定条件）{
      // 返回结果 or 退出搜索空间
    }
    for (const child of root.children) {
      dfs(child)
    }
}

而几乎所有的题目几乎都是二叉树，因此下面这个模板更常见。

1
2
3
4
5
6
7
function dfs(root) {
    if (满足特定条件）{
      // 返回结果 or 退出搜索空间
    }
    dfs(root.left)
    dfs(root.right)
}
分类

DFS 可细分为前中后序遍历。

前序遍历
1
2
3
4
5
6
7
8
function dfs(root) {
    if (满足特定条件）{
      // 返回结果 or 退出搜索空间
    }
    // 主要逻辑
    dfs(root.left)
    dfs(root.right)
}
后序遍历
1
2
3
4
5
6
7
8
function dfs(root) {
    if (满足特定条件）{
      // 返回结果 or 退出搜索空间
    }
    dfs(root.left)
    dfs(root.right)
    // 主要逻辑
}
中序遍历
1
2
3
4
5
6
7
8
function dfs(root) {
    if (满足特定条件）{
      // 返回结果 or 退出搜索空间
    }
    dfs(root.left)
    // 主要逻辑
    dfs(root.right)
}

广度优先遍历

广度优先遍历（Breadth-First-Search，以下简称 BFS）不同于 DFS，BFS 采用横向搜索的方式，在数据结构上通常采用队列结构。注意，DFS 我们借助的是栈来完成，而这里借助的是队列。

BFS 比较适合找最短距离/路径和某一个距离的目标。比如给定一个二叉树，在树的最后一行找到最左边的值。此题是力扣 513 的原题。这不就是求距离根节点最远距离的目标么？一个 BFS 模板就解决了。

广度优先遍历图解

算法流程
算法模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
const visited = {}
function bfs() {
	let q = new Queue()
	q.push(初始状态)
	while(q.length) {
		let i = q.pop()
        if (visited[i]) continue
        if (i 是我们要找的目标) return 结果
		for (i的可抵达状态j) {
			if (j 合法) {
				q.push(j)
			}
		}
    }
    return 没找到
}

BFS 可细分为带层的和不带层的。

树虽然只能从根开始访问，但是我们可以选择在访问完毕回来的时候做处理，还是在访问回来之前做处理，这两种不同的方式就是后序遍历和先序遍历。

三、题型

树的题目就三种类型，分别是：搜索类，构建类和修改类，而这三类题型的比例也是逐渐降低的，即搜索类的题目最多，其次是构建类，最后是修改类。这一点和链表有很大的不同，链表更多的是修改类。

搜索类

树的题目大多都涉及到搜索类。而搜索类只有两种解法，那就是 DFS 和 BFS。几乎所有的搜索类题目都可以方便地通过递归来解决，还有一小部分需要使用 BFS 借助队列（比如求二叉树任意两点的距离，树的距离其实就是最短距离，因此可以用 BFS 模板解决）。

搜索类的题目只要把握三个核心点，即开始点，结束点和目标即可。

回溯法求满足条件的所有路径

给定二叉树的根节点 root 和一个整数目标和 targetSum，找出所有从根节点到叶子节点路径总和等于给定目标和的路径

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} target
 * @return {number[][]}
 */

// 我的解答
var pathSum = function(root, target) {
    const res = []
    function deepIterate(node, nodeList) {
        if (!node) {
            return
        }
        nodeList.push(node.val)
        const total = nodeList.reduce((acc, item)=>{
            return acc + item
        }, 0)
        if (!(node.left || node.right) && total === target) {
            res.push(nodeList.slice(0))
        } else {
            deepIterate(node.left, nodeList)
            deepIterate(node.right, nodeList)
        }
        nodeList.pop()
    }
    
    deepIterate(root, [])
    return res
};

嘻嘻性能不错

构建类

修改类