数据结构：链表篇

发表于 更新于 分类于
本文字数： 5k 阅读时长 ≈ 5 分钟

各种数据结构，不管是队列，栈等线性数据结构还是树，图的等非线性数据结构，从根本上底层都是数组和链表。不管你用的是数组还是链表，用的都是计算机内存，物理内存是一个个大小相同的内存单元构成的。而数组和链表虽然用的都是物理内存，都是两者在对物理的使用上是非常不一样的。

一、和数组的差异

物理结构差异

数组是连续的内存空间，通常每一个单位的大小也是固定的，因此可以按下标随机访问。而链表则不一定连续，因此其查找只能依靠别的方式，一般是通过一个叫 next 指针来遍历查找。链表其实就是一个结构体。比如一个可能的单链表的定义可以是：

1
2
3
4
5
6
// data 是数据域，存放数据，next 指向下一个节点的指针
// 链表只有一个后驱节点 next，如果是双向链表还会有一个前驱节点 pre
interface ListNode<T> {
  data: T;
  next: ListNode<T>;
}

链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列节点（链表中每一个元素称为节点）组成，节点可以在运行时动态生成。

从上面的物理结构图可以看出数组是一块连续的空间，数组的每一项都是紧密相连的，因此如果要执行插入和删除操作就很麻烦。对数组头部的插入和删除时间复杂度都是$O(N)$，而平均复杂度也是$O(N)$，只有对尾部的插入和删除才是$O(1)$。简单来说，数组对查询特别友好，对删除和添加不友好。为了解决这个问题，就有了链表这种数据结构。链表适合在数据需要有一定顺序，但是又需要进行频繁增删除的场景。

使用差异

数组和链表作为线性的数组结构，在很多方面上都是相同的，只在细微的操作和使用场景上有差异而已。以遍历为例：

1
2
3
4
5
6
7
8
9
10
// 数组的遍历

for(int i = 0; i < arr.size();i++) {
    print(arr[i])
}

// 链表的遍历
for (ListNode cur = head; cur != null; cur = cur.next) {
    print(cur.val)
}

可以看出二者逻辑是一致的，只不过细微操作不一样。如果需要逆序遍历呢？

1
2
3
4
5
6
7
8
for(int i = arr.size() - 1; i > - 1;i--) {
    print(arr[i])
}

// 链表通常需要借助于双向链表。双向链表的力扣题目很少，大多数情况要拿到前驱节点，往往需要自行记录
for (ListNode cur = tail; cur != null; cur = cur.pre) {
    print(cur.val)
}

接下来说明怎么往末尾添加一个元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 数组
arr.push(1)

// 力扣通常使用如下的类来模拟链表节点
public class ListNode {
  int val;
  ListNode next;
  ListNode() {}
  ListNode(int val) { this.val = val; }
  ListNode(int val, ListNode next) { this.val = val; this.next = next; }
}
// 假设 tail 是链表的尾部节点
tail.next = new ListNode('lucifer')
tail = tail.next

由于两者存在的这些差异，在做题时不建议将链表换成数组，然后用数组做，这等于是否认了链表存在的价值。

二、基本操作

插入

插入只需要考虑要插入位置前驱节点和后继节点（双向链表的情况下需要更新后继节点）即可，其他节点不受影响，因此在给定指针的情况下插入的操作时间复杂度为 O(1)。这里给定指针中的指针指的是插入位置的前驱节点。

1
2
3
4
// 伪代码
temp = 待插入位置的前驱节点.next
待插入位置的前驱节点.next = 待插入指针
待插入指针.next = temp

如果没有给定指针，我们需要先遍历找到节点，因此最坏情况下时间复杂度为 O(N)。

删除

只需要将需要删除的节点的前驱指针的 next 指针修正为其下下个节点即可，注意考虑边界条件。

1
2
// 伪代码
待删除位置的前驱节点.next = 待删除位置的前驱节点.next.next

遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
// 迭代伪代码
当前指针 = 头指针
while 当前节点不为空 {
   print(当前节点)
   当前指针 = 当前指针.next
}

// 一个前序遍历的递归的伪代码
dfs(cur) {
    if 当前节点为空 return
    print(cur.val)
    return dfs(cur.next)
}

三、题型

链表的考点很单一，除了设计类题目，无非就是考察指针的修改（典型的就是链表反转）和链表的拼接。

链表反转

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
  # 翻转一个子链表，并且返回新的头与尾
  def reverse(self, head: ListNode, tail: ListNode, terminal: ListNode):
    cur = head
    pre = None
    while cur != terminal:
      # 留下联系方式
      next = cur.next
      # 修改指针
      cur.next = pre

      # 继续往下走
      pre = cur
      cur = next
    # 反转后的新的头尾节点返回出去
    return tail, head

其中 head 指的是需要反转的头节点，tail 是需要反转的尾节点，terminal 是 tail 后面的节点，用来保证 tail 也能被反转。不难看出，如果 head 是整个链表的头，tail 是整个链表的尾，那就是反转整个链表，否则就是反转局部链表。

链表拼接

链表常常涉及到穿来穿去（拼接）的操作，比如反转链表 II，再比如合并有序链表等。这正体现了链表的价值：无需连续的物理内存，以及对插入和删除的友好。可以使用“穿针引线”的思想来处理这类问题，这通常不是最优解，但是好理解，方便书写，不易出错，推荐新手用。以反转链表的中间一部分为例进行说明。

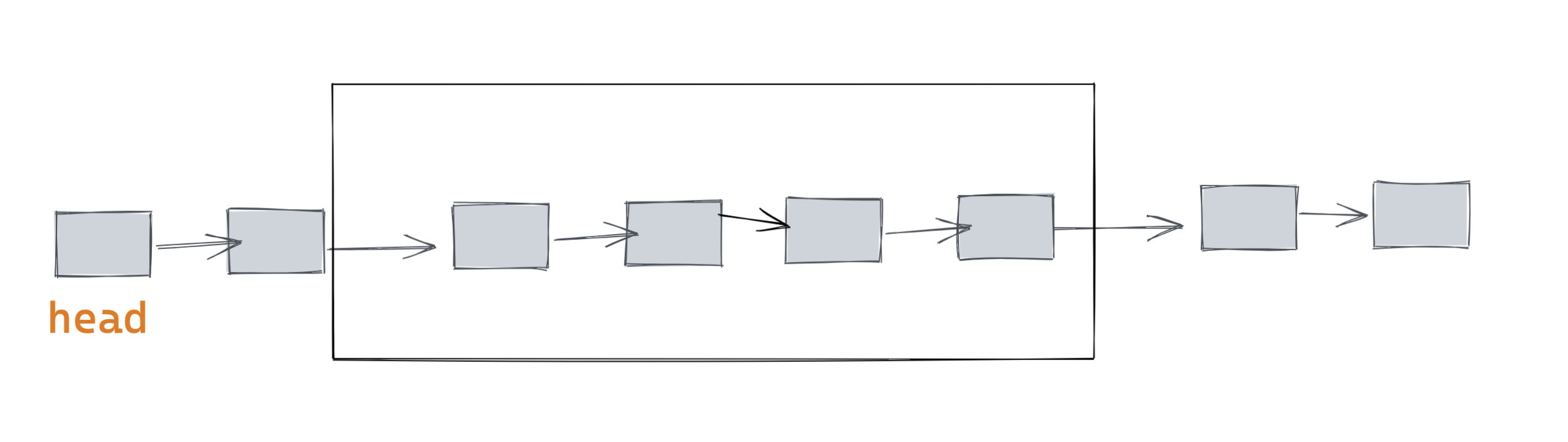
20230418111629

反转在前文已说明怎么实现，在这里不再赘述如何反转，而着重于如何将反转后的链表进行拼接。

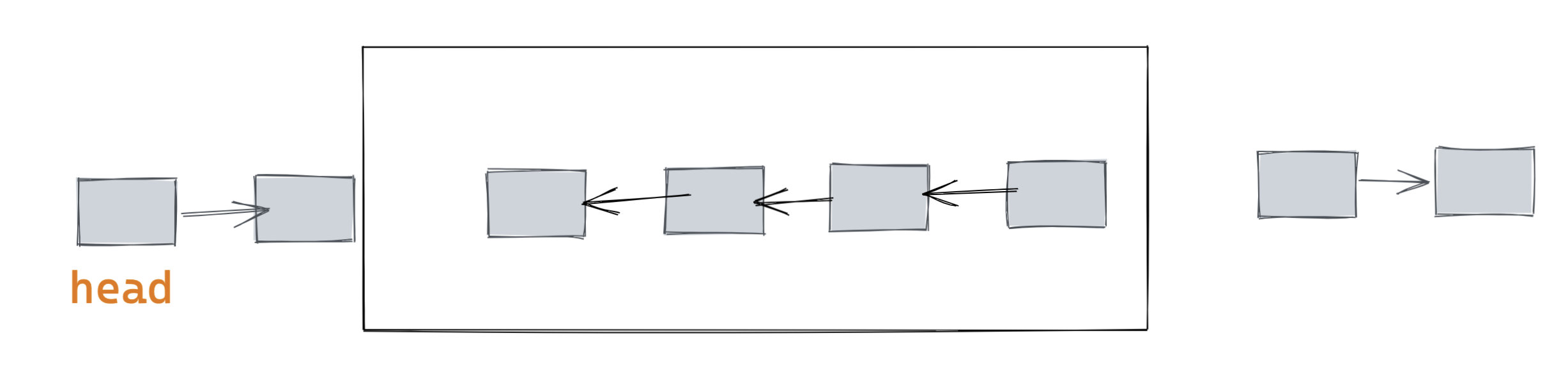
20230418112002

我们想要的效果是这样的：

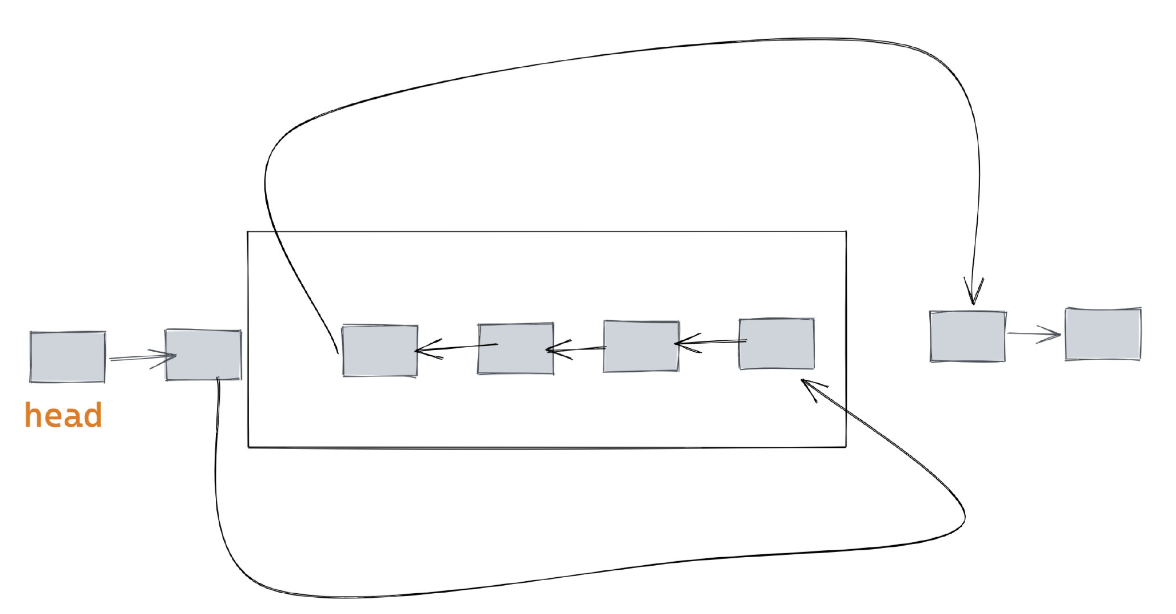
20230418112056

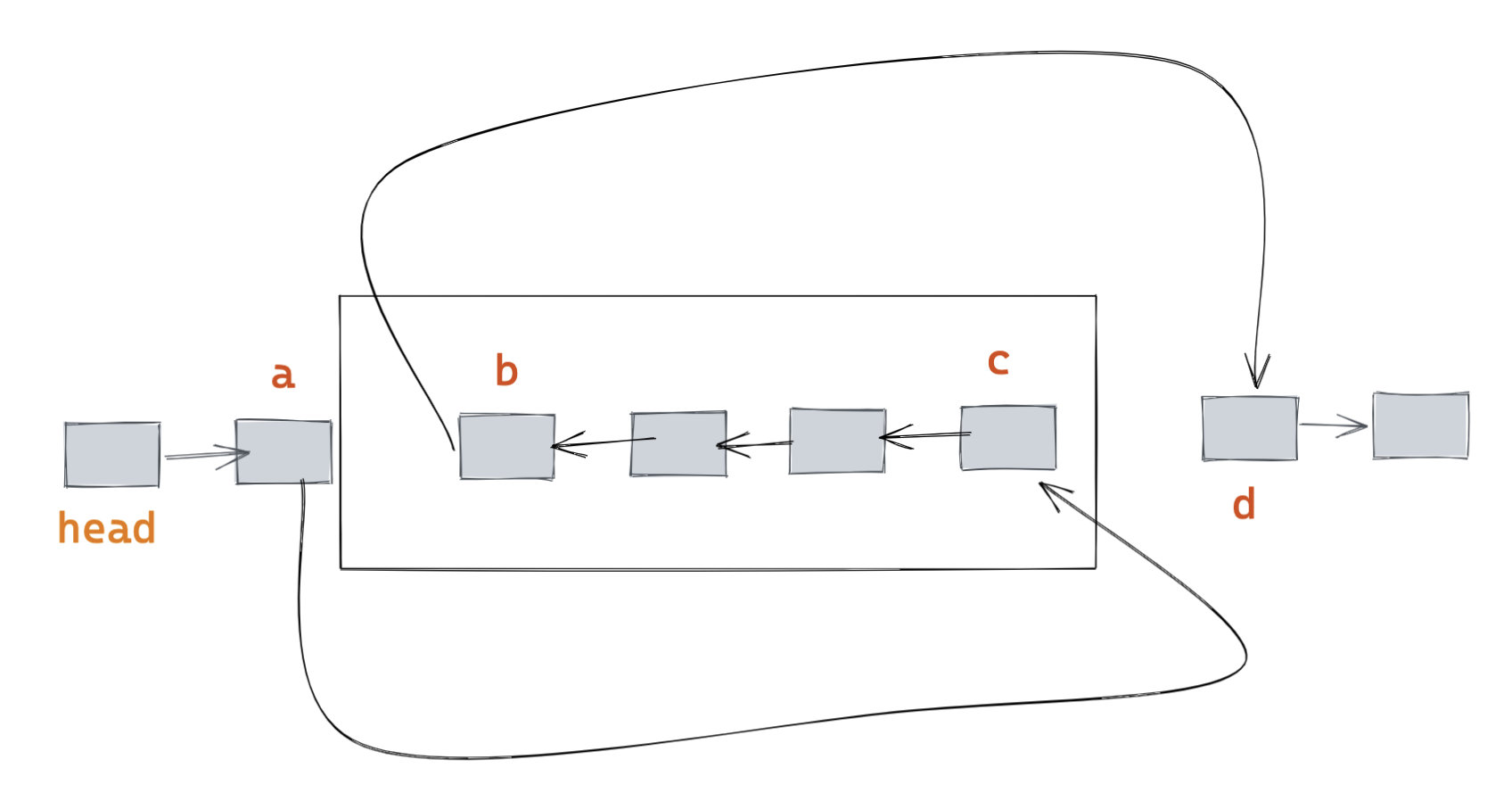
那怎么达到图上的效果呢？我的做法是从左到右给断点编号。如图有两个断点，共涉及到四个节点。于是我给它们依次编号为 a，b，c，d。
其实 a，d 分别是需要反转的链表部分的前驱和后继（不参与反转），而 b 和 c 是需要反转的部分的头和尾（参与反转）。
因此除了 cur，多用两个指针 pre 和 next 即可找到 a，b，c，d。
找到后就简单了，直接穿针引线。

1
2
a.next = c
b.next = d

20230418112149

在 25. K 个一组翻转链表，61. 旋转链表 和 92. 反转链表 II 都用了这个方法。

快慢指针应用

快慢指针是双指针的一种典型用法，通常控制两个指针以不同的速度移动来解决问题。采用快慢指针解决问题往往都很巧妙。要想理解这个解决办法需要先了解 Floyd 判圈算法。

Floyd 判圈算法又称为龟兔赛跑算法（Tortoise and Hare Algorithm）。乌龟跑得慢、兔子跑得快。乌龟和兔子在赛跑，如果存在环的话，兔子必然会追上乌龟。

我们把乌龟比作慢指针、兔子比作快指针同时在链表中移动。跑步和指针移动不太相同的是，跑步的路程是连续的，快指针一次移动两个节点是不连续的。又反过来想一下如果链表中存在环，那最小的环也需要两个节点，所以对于是否有环来说快指针一次移动两个节点也是不会错过任何一个环的。而且环的节点不管是奇数还是偶数个，快指针也最终会和慢指针在某个节点重合。

判断链表是否有环

给定一个链表的头节点 head，判断链表中是否有环

1
2
3
4
5
6
7
8
9
10
var hasCycle = function(head) {
    if(head === null) return false
    let slow = head, fast = head.next
    while(fast && fast.next) {
        if (slow.next === fast.next.next) return true
        slow = slow.next
        fast = fast.next.next
    }
    return false
};
寻找链表中环的路口

给定一个链表的头节点 head，返回链表开始入环的第一个节点。如果链表无环，则返回 null

这道题和上题一样，通常有哈希表、快慢指针两种解法。在此主要分析快慢指针的解法：定义两个指针，一个移动的慢叫慢指针，一个移动的快叫快指针。慢指针在链表中一次移动一个节点，快指针在链表中一次移动两个节点，如果两个指针最终相遇了，说明有环；如果快指针顺利到达了链表的终点说明没有环。

如下图所示，设链表中环外部分长度为 a。慢指针进入环后，又走了 b 的距离与快指针相遇。此时，快指针已经走完了环的 n 圈，因此它走过的总距离为 a + n*(b+c) + b，即 a + (n+1)*b + n*c。

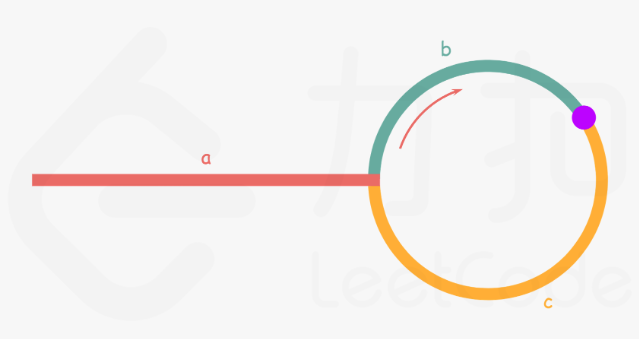
根据题意，任意时刻，快指针走过的距离都为慢指针的两倍。因此，我们有

a + (n+1)*b + n*c === 2*(a+b)

化简得 a === c + (n-1)*(b+c)，根据这个关系可以发现：从相遇点到入环点的距离加上 n-1 圈的环长，恰好等于从链表头部到入环点的距离。因此，当快慢指针相遇时，我们再额外使用一个指针 ptr。起初，它指向链表头部；随后，它会和慢指针每次向后移动一个位置。最终，它们会在入环点相遇。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
var detectCycle = function(head) {
    if (head === null) {
        return null;
    }
    let slow = head, fast = head;
    while (fast !== null) {
        slow = slow.next;
        if (fast.next !== null) {
            fast = fast.next.next;
        } else {
            return null;
        }
        if (fast === slow) {
            let ptr = head;
            while (ptr !== slow) {
                ptr = ptr.next;
                slow = slow.next;
            }
            return ptr;
        }
    }
    return null;
};
寻找链表的中间节点

给定单链表的头节点 head，找出并返回链表的中间节点

这道题有多种解法，但是快慢指针的解法十分巧妙。我们定义两个指针：一个移动的慢叫慢指针，一个移动的快叫快指针。慢指针在链表中一次移动一个结点，快指针在链表中一次移动两个结点。因为快指针移动的距离始终是慢指针的两倍，所以当快指针移动到链表尾部时，慢指针刚好在链表中间位置。

1
2
3
4
5
6
7
8
var middleNode = function(head) {
    slow = fast = head;
    while (fast && fast.next) {
        slow = slow.next;
        fast = fast.next.next;
    }
    return slow;
};
寻找链表倒数第 N 个结点

这道题有多种解法，但是快慢指针的解法十分巧妙。我们定义两个指针：两个指针每次移动一个结点。我们让其中一个指针先移动 n 个结点，先移动的这个指针我们叫它快指针，另外一个叫慢指针。然后两个指针同时移动。因为移动速度相同所以两个指针之间的距离始终是 n，当快指针到达链表尾部时，慢指针刚好指向了链表的倒数第 n 个结点。

1
2
3
4
5
6
7
8
9
10
11
var findNthNode = function(head, n) {
    slow = fast = head;
    for (let i = 0; i < n+1; i++) {
        fast = fast.next;
    }
    while(fast !== null) {
        fast = fast.next;
        slow = slow.next;
    }
    return slow;
}

四、题目推荐

参考资料